概要: )=ax12+x1+ax22+x2-2[a( )2+ ]= a(x1-x2)2≥0.∴f( )≤ [f(x1)+f(x2)],∴f(x)是凹函数.19.(1)证明:令x=y=0,则f(0)+f(0)=f(0),故f(0)=0.令y=-x,则f(x)+f(-x)=f( )=f(0)=0.∴f(-x)=-f(x),即函数f(x)是奇函数.(2)证明:设x1 ).∵x10,-1 <0,∴f( )>0,即f(x1)>f(x2).∴函数f(x)在(-1,1)上是减函数.20.解:(1)设P(x1,y1),Q(x2,y2)(x1≠x2)是函数f(x)= 的图象上的两个“稳定点”,∴ ,即有x12+ax1=3x1-1(x1≠-a),x22+ax2=3x2-1(x2≠-a).有x12+(a-3)x1+1=0(x1≠-a),x22+(a-3)x2+1=0(x2≠-a).&the
高一数学必修一单元测试,标签:小学数学知识点,http://www.85jc.com
)
=ax12+x1+ax22+x2-2[a(
)2+
]
=
a(x1-x2)2≥0.∴f(
)≤
[f(x1)+f(x2)],∴f(x)是凹函数.
19.(1)证明:令x=y=0,则f(0)+f(0)=f(0),故f(0)=0.
令y=-x,则f(x)+f(-x)=f(
)=f(0)=0.∴f(-x)=-f(x),即函数f(x)是奇函数.
(2)证明:设x1
).
∵x10,-1
<0,∴f(
)>0,
即f(x1)>f(x2).∴函数f(x)在(-1,1)上是减函数.
20.解:(1)设P(x1,y1),Q(x2,y2)(x1≠x2)是函数f(x)=
的图象上的两个“稳定点”,
∴
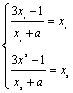
,即有x12+ax1=3x1-1(x1≠-a),x22+ax2=3x2-1(x2≠-a).
有x12+(a-3)x1+1=0(x1≠-a),x22+(a-3)x2+1=0(x2≠-a).
∴x1、x2是方程x2+(a-3)x+1=0两根,且∵x1, x2≠-a,∴x≠-a,
上一页 [1] [2] [3] [4] [5] [6] [7] 下一页
最新更新