概要:∴方程x2+(a-3)x+1=0有两个相异的实根且不等于-a.∴ ∴a>5或a<1且a≠- .∴a的范围是(-∞,- )∪(- ,1)∪(5,+∞). (2)∵f(x)是R上的奇函数,∴f(-0)=-f(0),即f(0)=0.∴原点(0,0)是函数f(x)的“稳定点”,若f(x)还有稳定点(x0,y0),则∵f(x)为奇函数,f(-x0)=-f(x0),f(x0)=x0,∴f(-x0)=-x0,这说明:(-x0,-x0)也是f(x)的“稳定点”.综上所述可知,f(x)图象上的“稳定点”除原点外是成对出现的,而且原点也是其“稳定点”,∴它的个数为奇数.上一页 [1] [2] [3] [4] [5] [6] [7]
高一数学必修一单元测试,标签:小学数学知识点,http://www.85jc.com∴方程x2+(a-3)x+1=0有两个相异的实根且不等于-a.
∴
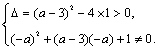
∴a>5或a<1且a≠-
.
∴a的范围是(-∞,-
)∪(-
,1)∪(5,+∞). (2)∵f(x)是R上的奇函数,
∴f(-0)=-f(0),即f(0)=0.∴原点(0,0)是函数f(x)的“稳定点”,若f(x)还有稳定点(x0,y0),则∵f(x)为奇函数,f(-x0)=-f(x0),f(x0)=x0,∴f(-x0)=-x0,这说明:(-x0,-x0)也是f(x)的“稳定点”.综上所述可知,f(x)图象上的“稳定点”除原点外是成对出现的,而且原点也是其“稳定点”,
∴它的个数为奇数.
上一页 [1] [2] [3] [4] [5] [6] [7]
最新更新