概要: 教师提出问题,引导学生利用度量工具(量角器或几何画板)动手实验,进行度量,发现结论.由学生总结发现的规律:同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.教师再利用几何画板从动态的角度进行演示,验证学生的发现.教师可从以下几个方面演示,让学生观察圆周角的度数是否发生改变,同弧所对的圆周角与圆心角的关系有无变化:(1)拖动圆周角的顶点使其在圆周上运动;(2)改变圆心角的度数;3.改变圆的半径大小.本次活动中,教师应当重点关注:(1)学生是否积极参与活动;(2)学生是否度量准确,观察、发现的结论是否正确.活动2的设计是为 引导学生发现.让学生亲自动手,利用度量工具(如半圆仪、几何画板)进行实验、探究,得出结论.激发学生的求知欲望,调动学生学习的积极性.教师利用几何画板从动态的角度进行演示,目的是用运动变化的观点来研究问题,从运动变化的过程中寻找不变的关系.[活动3]问题(1)在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况?(2)当圆心在圆周角的一边上时,如何证明活动2中所发现
九年级上册《圆周角》教学设计,标签:教学设计,http://www.85jc.com

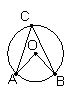
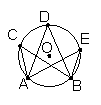
教师提出问题,引导学生利用度量工具(量角器或几何画板)动手实验,进行度量,发现结论.
由学生总结发现的规律:同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.
教师再利用几何画板从动态的角度进行演示,验证学生的发现.教师可从以下几个方面演示,让学生观察圆周角的度数是否发生改变,同弧所对的圆周角与圆心角的关系有无变化:
(1)拖动圆周角的顶点使其在圆周上运动;
(2)改变圆心角的度数;3.改变圆的半径大小.
本次活动中,教师应当重点关注:
(1)学生是否积极参与活动;
(2)学生是否度量准确,观察、发现的结论是否正确.
活动2的设计是为 引导学生发现.让学生亲自动手,利用度量工具(如半圆仪、几何画板)进行实验、探究,得出结论.激发学生的求知欲望,调动学生学习的积极性.教师利用几何画板从动态的角度进行演示,目的是用运动变化的观点来研究问题,从运动变化的过程中寻找不变的关系.
[活动3]
问题
(1)在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况?
(2)当圆心在圆周角的一边上时,如何证明活动2中所发现的结论?
(3)另外两种情况如何证明,可否转化成第一种情况呢?
教师引导学生,采取小组合作的学习方式,前后四人一组,分组讨论.
教师巡视,请学生回答问题.回答不全面时,请其他同学给予补充.
教师演示圆心与圆周角的三种位置关系.
本次活动中,教师应当重点关注:
(1)学生是否会与人合作,并能与他人交流思维的过程和结果.
(2)学生能否发现圆心与圆周角的三种位置关系.学生是否积极参与活动.
教师引导学生从特殊情况入手证明所发现的结论.
学生写出已知、求证,完成证明.
学生采取小组合作的学习方式进行探索发现,教师观察指导小组活动.启发并引导学生,通过添加辅助线,将问题进行转化.教师讲评学生的证明,板书圆周角定理.
本次活动中,教师应当重点关注:
(1)学生是否会想到添加辅助线,将另外两种情况进行转化
(2)学生添加辅助线的合理性.
(3)学生是否会利用问题2的结论进行证明.
数学教学是在教师的引导下,进行的再创造、再发现的教学.通过数学活动,教给学生一种科学研究的方法.学会发现问题,提出问题,分析问题,并能解决问题.活动3的安排是让学生对所发现的结论进行证明.培养学生严谨的治学态度.
问题1的设计是让学生通过合作探索,学会运用分类讨论的数学思想研究问题.培养学生思维的深刻性.
问题2、3的提出是让学生学会一种分析问题、解决问题的方式方法:从特殊到一般.学会运用化归思想将问题转化.并启发培养学生创造性的解决问题
[活动4]
问题
(1)半圆(或直径)所对的圆周角是多少度?


最新更新