1. 高中数学《二倍角的正弦、余弦、正切》教学设计

2. [11-19 17:56:12]   来源：http://www.85jc.com  数学教学设计   阅读：8652次

概要：二、引导探究、深化认识1、回忆推导过程，让学生明确二倍角公式是和角公式的特殊情形。知道二者之间的联系2、(探索性提问)对 ： 中的平方联想到 ， 有无其他变式?(学生探索、总结得出两种变式： )3、(深化性提问)：有了这组二倍角公式，我们是否可以放心大胆的应用呢?(学生：不能，要注意公式成立的条件)引导学生联想和角公式的条件，利用类比的方法，探索出二倍角公式的条件 指出：尤其注意 成立的条件【设计意图：引导学生应用联想、类比的教学思想、得出公式成立的条件】4、(探索性提问)在 中，当左边的 时，虽然右边的 不存在，但左边的 存在，能否用上一页 [1] [2] [3] [4] [5] [6] [7] [8] 下一页

高中数学《二倍角的正弦、余弦、正切》教学设计,标签：教学设计,http://www.85jc.com

　　二、引导探究、深化认识

　　1、回忆推导过程，让学生明确二倍角公式是和角公式的特殊情形。知道二者之间的联系

　　2、(探索性提问)对

　　

 

　　：

　　

 

　　中的平方联想到

　　

 

　　，

　　

 

　　有无其他变式?

　　(学生探索、总结得出两种变式：

　　

 

　　)

　　3、(深化性提问)：有了这组二倍角公式，我们是否可以放心大胆的应用呢?

　　(学生：不能，要注意公式成立的条件)

　　引导学生联想和角公式的条件，利用类比的方法，探索出二倍角公式的条件

　　

 

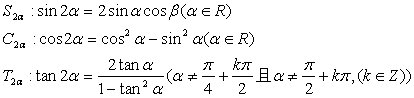
　　指出：尤其注意

　　

 

　　成立的条件

　　【设计意图：引导学生应用联想、类比的教学思想、得出公式成立的条件】

　　4、(探索性提问)在

　　

 

　　中，当左边的

　　

 

　　时，虽然右边的

　　

 

　　不存在，但左边的

　　

 

　　存在，能否用

　　

上一页  [1] [2] [3] [4] [5] [6] [7] [8]  下一页

Tag:数学教学设计，教学设计，数学学习 - 数学教研 - 数学教学设计

上一篇：高中数学必修4《二倍角的正弦、余弦、正切》教学设计